钢木混合结构在不同性能水准下的层间位移角限值

1 引言

木结构具有绿色环保、抗震性能好等优势，但传统的木结构由于其自身特点，大多适用于2 ～ 3 层建筑，很难适应我国现阶段城市人口密度较高的现状[1]。因此，需要探寻符合我国国情的多高层木或木混合结构体系形式。

笔者结合钢结构和轻型木结构的特点，提出了一种在钢框架梁上铺设钢木混合楼（屋）盖、在钢框架柱间设置轻型木剪力墙的新型多层钢木混合结构[2]。通过对钢木混合结构进行试验研究和数值模拟发现，该结构抗震性能较好[3]，具有一定的应用前景；內填轻型木剪力墙可以有效地提高结构的抗侧承载力和刚度，增大轻型木剪力墙和钢框架的初始抗侧刚度比λ 可以提高结构的抗震性能[2]；合理的钢木连接方式可以确保钢框架和木剪力墙的协同工作性能[4]。

结构的层间位移角可以较好地反映结构整体在地震作用下的安全情况，同时能反映结构主要构件的破坏情况[5-6]，因此基于结构层间位移角的性能目标被逐渐应用在结构抗震设计中。但目前钢木混合结构在不同性能水准下的层间位移角限值仍需进一步研究。

为确定钢木混合结构在不同性能水准下的层间位移角限值，设计120 个不同构造的钢木混合抗侧力体系，在OpenSees 中对其进行建模以及推覆模拟，获得具有95% 保证率的钢木混合抗侧力体系屈服层间位移角；设计不同木剪力墙和钢框架抗侧刚度比的三层和六层的钢木混合结构，在OpenSees 中对其进行增量动力分析，获得具有95% 保证率的钢木混合结构倒塌极限状态层间位移角。结合已有试验结论，给出钢木混合结构立即居住和防止倒塌层间位移角限值的建议取值。

2 钢木混合结构有限元模拟方法

采用弹塑性有限元程序OpenSees 对钢木混合结构进行模拟，模拟示意图如图1 所示。其中，钢框架采用基于刚度的纤维梁单元进行模拟，并采用考虑了随动强化特性Steel01 材料；轻型木剪力墙采用TwoNodeLink单元进行模拟，利用单轴材料Pinching4 模拟轻型木剪力墙的捏缩效应[7]。

由于高强螺栓连接可以保证木剪力墙充分参与协同工作[8]，因此本文的钢木连接方式采用高强螺栓连接，即钢框架和木剪力墙之间可认为完全连接。

图1 钢木混合结构模拟示意图

3 立即居住层间位移角限值

3.1 分析对象

数值模拟分析对象为单层单榀的钢木混合抗侧力体系，如图2 所示。其中钢框架由热轧H 型钢拼装而成，钢材等级为Q235B，钢框架和木剪力墙间采用高强螺栓连接。

由于木剪力墙与钢框架的初始刚度比λ 对钢木混合结构的抗侧力性能影响较大[9]，将λ 作为数值模拟分析的参数之一，设计了λ 取值分别为1.0，1.5，2.0，2.5和3.0 的钢木混合抗侧力体系，以衡量不同钢木混合抗侧力体系中木剪力墙和钢框架的相对强弱。λ 的定义见式(1)。

此外，为考虑尺寸对钢木混合抗侧力体系抗侧性能的影响，本文结合工程实际中的常用尺寸，设计了不同高度（分别为2.4m，3.0m，3.6m，4.2m，4.8m）和跨度（分别为3.6m，4.8m，6.0m，7.2m）的钢木混合抗侧力体系，钢框架的分组及详细信息见表1。其中，每组包含5 种不同λ 的钢木混合抗侧力体系，即共设计了120 个钢木混合抗侧力体系。

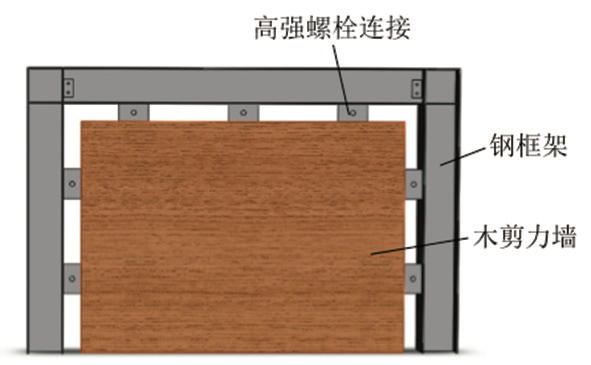
图2 参数分析模型示意图

表1 钢木混合抗侧力体系分析参数

3.2 边界条件及加载制度

钢木混合抗侧力体系的钢框架柱脚假定为刚接，梁柱节点假定为完全刚接。对钢木混合抗侧力体系进行位移控制的推覆模拟，加载点为钢木混合抗侧力体系左上角梁柱节点。

3.3 分析结果

常见的木结构等效屈服点的定义主要包括以下五种：Karacabeyli and Ceccotti 法（简称K&C 法）[10]、CEN 法[11]、CSIRO 法[12]、Equivalent Energy Elastic Plastic 法（简称EEEP 法）[13] 和Yasumura and Kawai法（简称Y&K 法）[14]。其中，CEN 法和EEEP 法定义的屈服点常偏离荷载—位移曲线，CSIRO 和K&C 法定义的屈服点可能会低估结构的屈服位移，而Y&K 法可以有效地避免上述问题[15]，因此本文采用Y&K 定义钢木混合抗侧力体系的屈服点。

图3 为120 个钢木混合抗侧力体系的屈服位移角的频数直方图，在Minitab 软件中对120 组钢木混合抗侧力体系的屈服位移角的概率分布进行显著性水平a=0.05的拟合优度检验，可得钢木混合抗侧力体系的等效屈服位移角服从对数正态分布。

图3 屈服位移角频率直方图

图4 钢木混合结构屈服位移角概率密度分布图

绘制由120 组屈服位移角数据拟合得到的对数正态分布的概率密度曲线，如图4 所示。可以得到，具有95% 保证率的钢木混合抗侧力体系屈服位移角为0.48%。

结合钢木混合结构单层足尺试验的试验现象[16]，建议钢木混合结构立即居住性能水准层间位移角限值取为0.5%。

4 防止倒塌层间位移角限值

4.1 分析对象

根据《钢结构设计规范》[17] 和《建筑抗震设计规范》[18] 设计了层数分别为三层和六层钢木混合结构，拟建场地的设防烈度为8 度，场地类别为第II 类第二组。各层层高均选为3.3m，楼面活荷载为2.5kN/m²，屋面活荷载为0.5kN/m²，按工程实际楼屋面做法计算得到楼面恒荷载和屋面恒荷载分别为4.0kN/m²、1.8kN/m²，钢材选用Q235B。

为考虑木剪力墙与钢框架抗侧初始刚度比λ 的影响，考虑了三种不同刚度比λ（分别取1.0，2.0 和3.0）与前述两种层数钢木混合结构的组合，即共设计了六种不同的钢木混合结构。六组钢木混合结构的标准层平面布置图如图5 所示，其中钢构件截面如表2 所示，ksteel通过pushover 分析得到，通过设计轻型木剪力墙的覆面板厚度、钉类型以及钉间距等参数即可获得所需刚度的轻木剪力墙。

4.2 地震记录选择

选取地震记录时，需考虑结构所在的场地条件以及由地震记录转化的加速度反应谱与规范设计反应谱的匹配程度[19]。本文选取10 条地震记录作为增量动力分析（简称IDA）的地震输入，地震记录如表3 所示。

图5 结构平面布置图

表2 钢构件截面

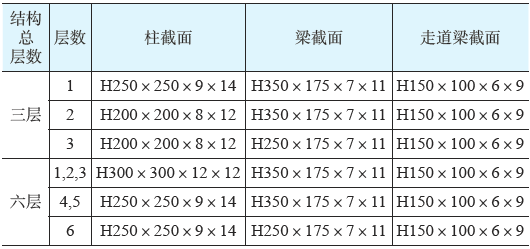
表3 分析中应用的地震动记录

4.3 分析结果

对IDA 结果进行分析，采用FEMA350[20] 推荐方法判断结构倒塌极限状态，即取IDA 曲线斜率下降至弹性阶段斜率Ke 的20% 的点和最大层间位移角为10%的点中数值较小的点作为结构倒塌极限状态点。

对结构倒塌极限状态层间位移角进行统计并绘制频数直方图，如图6 所示。在Minitab 软件中对60 组钢木混合抗侧力体系的倒塌极限状态层间位移角的概率分布进行显著性水平a=0.05 的拟合优度检验，可得钢木混合抗侧力体系的倒塌极限状态层间位移角服从对数正态分布。

图6 倒塌极限状态层间位移角频数直方图

图7 为由60 组倒塌极限状态层间位移角数据拟合得到的对数正态分布的概率密度曲线，可以看出，具有95% 保证率时钢木混合结构的倒塌极限状态层间位移角为2.433%。

图7 倒塌极限状态层间位移角概率密度分布图

结合钢木混合结构单层足尺试验的试验现象[16]，建议钢木混合结构防止倒塌性能水准层间位移角限值取为2.5%。

5 结论

本文设计了120 个不同构造的钢木混合抗侧力体系，在OpenSees 中对其进行建模及单调加载模拟，获得具有95% 保证率的钢木混合抗侧力体系屈服层间位移角。设计不同初始刚度比的三层和六层的钢木混合结构，在OpenSees 中对其进行增量动力分析，获得具有95% 保证率的钢木混合结构倒塌极限状态层间位移角。结合已有试验结论，建议钢木混合结构立即居住和防止倒塌层间位移角限值分别取为0.5% 和2.5%。

参考文献

[1] 何敏娟, LAM Frank, 杨军, 等. 木结构设计[M].北京: 中国建筑工业出版社, 2008: 1-22.

[2] HE M, LI Z, LAM F, et al. Experimental Investigation on Lateral Performance of Timber-Steel Hybrid Shear Wall Systems [J]. Journal of Structural Engineering, 2013, 140(6):04014029.

[3] He M, Luo Q, Li Z, et al. Seismic performance evaluation of timber-steel hybrid structure through largescale shaking table tests[J]. Engineering Structures, 2018,175: 483-500.

[4] Li Z, He M, Lam F, et al. Finite element modeling and parametric analysis of timber–steel hybrid structures[J]. The Structural Design of Tall and Special Buildings, 2014, 23(14): 1045-1063.

[5] Rosowsky DV, Ellingwood, BR. Performancebased engineering of wood frame housing: Fragility analysis methodology[J]. Journal of Structural Engineering, 2002, 128 (1): 32-38.

[6] Rosowsky DV. Reliability-based seismic design of wood shear walls[J]. Journal of Structural Engineering, ASCE, 2002, 128(11): 1439-1453.

[7] LI Z, HE M, WANG X, et al. Seismic performance assessment of steel frame infilled with prefabricated wood shear walls [J]. Journal of Constructional Steel Research, 2017, 140:62-73.

[8] 何敏娟, 董文晨, 李征. 往复荷载下两种连接方式钢木混合墙体抗侧性能研究[J]. 建筑结构, 2018(10).

[9] Li Z, He M, Lam F, et al. Load-sharing mechanismin timber-steel hybrid shear wall systems[J]. Frontiers of Structural and Civil Engineering, 2015, 9(2): 203-214.

[10] Karacabeyli E, Ceccotti A. Quasi-static reversedcyclic testing of nailed joints[C]. Proc. Int.Council for Build. Res. Studies and Documentation, Working Commission W18-Timber Structure, Meeting 28, Copenhagen, Denmark, 1996.

[11] Ceccotti A. Timber connections under seismic actions[J]. Timber engineering–STEP 1. 1st Edition, 1995,1(1): C17.

[12] Timber evaluation of mechanical joint systems-Part 3: Earthquake loading[S]. Melbourne: Commonwealth Scientific and Industrial Research Organization, 1996.

[13] ASTM E 2126-05. Standard Test Method for Cyclic (Reversed) Load Test for Shear Resistance of Walls for Buildings[S]. Pennsylvania: American Society for Testing and Materials, 1996.

[14] Yasumura M, Kawai N. Estimating seismic performance of wood-framed structures[C]. Proceedings of 1998 I.W.E.C., Switzerland, 1998: 564-571.

[15] Muñoz W, Mohammad M, Salenikovich A, et al. Determination of yield point and ductility of timber assemblies: in search for a harmonised approach[J].Engineered Wood Products Association, 2008.

[16] 李征. 钢木混合结构竖向抗侧力体系抗震性能研究[D]. 上海: 同济大学. 2014.

[17] 中华人民共和国国家标准. 钢结构设计标准(GB50017-2017)[S]. 北京: 中国建筑工业出版社, 2018.

[18] 中华人民共和国国家标准. 建筑抗震设计规范(GB 50011-2010)[S]. 北京: 中国建筑工业出版社, 2016.

[19] 曲哲, 叶列平, 潘鹏. 建筑结构弹塑性时程分析中地震动记录选取方法的比较研究[J]. 土木工程学报, 2011,44(7):10-21.

[20] FEMA. Recommended seismic design criteria for new steel moment-frame buildings[R]. Washington, DC: Federal Emergency Management Agency, No. FEMA-350, 2000.

作者

同济大学建筑工程系   王希珺  李征

福州大学土木工程学院   Briseghella Bruno Nuti Camillo