紊流模型对建筑物绕流的影响

1 前言

建筑物室内自然通风问题的研究有重要的意义，其节能效益也越来越受重视。目前对自然通风问题的研究通常有两种方法: 在设计阶段采用风洞试验和对已建建筑直接测量数据，这两种方法都需要消耗较多的人力物力。近年来随着计算流体力学(CFD) 的发展，采用计算流体力学(CFD) 方法对自然通风问题进行研究成了另一种选择，而建筑物绕流计算结果的准确性决定着自然通风CFD 计算结果的精度，因此国内外很多学者都对建筑绕流问题进行了研究。对绕流问题研究的方法根据紊流模型的不同可以分为雷诺平均(RANS) 模型与大涡模拟(LES) 模型，前者利用对纳维- 斯托克斯方程进行时间平均的方法，后者则是利用滤波函数对纳维- 斯托克斯方程进行空间过滤的方法。

RANS 模型分为稳态RANS 模型(S-RANS) 与非稳态RANS 模型 (U-RANS)。张维[1] 最早在国内采用S-RANS 中的标准k-ε 模型对建筑物扰流进行计算，并利用风洞结果对标准k-ε 模型进行了验证。日本建筑协会(AIJ) 的用户手册[2] 利用采用稳态RANS 与LES 计算了2:1:1 的建筑绕流并与试验值进行了对比，给出了合理的计算域大小、边界条件以及推荐计算格式；Tominaga 和Stathopoulos[3] 对比了稳态RANS 模型中RNG k-ε 模型与标准k-ε 模型，其中RNG k-ε 模型为Yakhot [4] 提出，其紊流模型的系数并不是可调节系数，而是由理论推导的常数，发现RNG k-ε 的计算在尾涡区与实验值更接近，但稳态RANS 模型在计算建筑绕流依然存在着如脱离涡的距离会较大，迎风面的紊流能量较大的问题。Tominaga[5] 之后的研究对比了非稳态RANS 模型与稳态RANS 模型，发现非稳态RANS模型在建筑后方的流场分布要好于稳态RANS。上述研究较多地探讨了对于不同非稳态RANS 模型的平均值的准确性，但对于非稳态RANS 模型的脉动速度的探讨则较少。

一方面，大涡模拟（LES）模型具有可以模拟瞬时流动状态的功能，Werner 和Wengle[6] 将LES 应用到方柱中绕流的计算, 并与实验值进行了验证。Tominaga[7]采用LES 的标准Smagorinsky 亚格子模型以及采用周期循环的方式生成模拟自然进风紊流边界与无紊流模拟自然风边界进行对比，发现无紊流自然风的边界条件会在建筑后部产生更少的涡，模拟结果与实际值的差距也更大，而加入采用周期循环的方式生成模拟自然进风紊流边界的LES 结果与实验值吻合的更好。但是采用周期循环的方式生成模拟自然进风紊流边界的方法，由于数值误差或者人工产生的扰动可能会被网格粘度与数值粘度耗散掉，其产生紊流的时间会很长[8]，因此会需要较多的计算资源。

基于对上述建筑绕流的雷诺平均(RANS) 模型与大涡模拟(LES) 模型的讨论，本文利用开源计算流体力学软件(OpenFOAM)，对于建筑绕流的非稳态RANS 模型的脉动速度进行了深入探讨并推导了脉动速度的计算公式。同时，为了探讨不同非稳态RANS 模型对模拟结果的影响，本文对非稳态RANS 模型的RNG k-ε 和SST k-ω 模型[9] 进行对比并讨论了这两种模型的适用性。

另一方面，对于LES 模型而言，如何设置建筑绕流的自然风流入边界的紊流量是能否精确地进行LES模拟的关键。本文为了避免采用周期循环方式，尝试植入了一种人造紊流模拟自然风流入边界，并利用这种人造紊流模拟自然风流入边界进行了建筑绕流的LES 模拟，同时将模拟结果和Meng 和hibi[10] 的风洞实验值进行了对比验证。

2 计算模型

2.1 物理模型

本次计算为了与文献[10] 的风洞试验数据做对比，也选用了物理模型为2:1:1 建筑物绕流模型如图1 所示，给定了了进口速度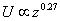, 建筑物长宽高分别为0.08m、0.08m、0.16m，其雷诺数，其中Ub 为半高出的进口速度，υ 为空气粘度。

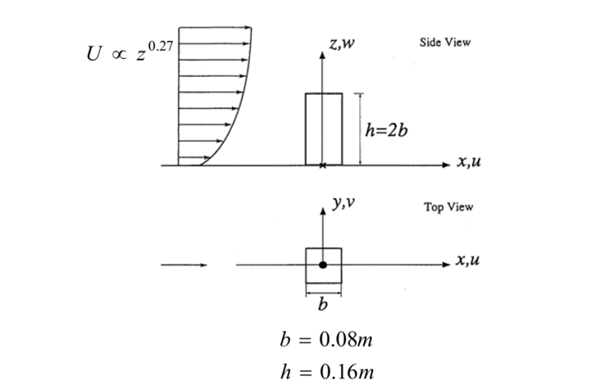
图1 建筑物绕流的物理模型

2.2 计算域

计算域采用了Liu 和Niu[11] 建议的大小，如图2 所示, 计算域的大小为20b×13b×12b，其中b 即为建筑的宽度为0.08m。

图2 计算域的大小设置

2.3 紊流模拟方法

RANS 模型为对纳维- 斯托克斯方程求时间平均后得到的紊流模型，对于任一物理量φ 其时间平均值为:

LES (Large-Eddy Simulation) 模型为对纳维- 斯托克斯方程进行空间滤波后得到的紊流模型，对于任一物理量φ 执行空间滤波操作:

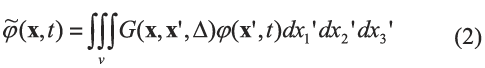
其中为滤波函数，Δ 为截止尺度。在本文计算中使用的是有限体积法，因此直接采用隐式滤波，利用网格进行滤波，得到的平均值即为网格内的平均值。

对于RANS 和LES 方法，其连续方程与纳维- 斯托克斯方程可以总结为

2.4 计算网格的划分

为了设定合理的网格分布，本文参考了Spalart[12]的分区方法，将建筑物绕流分为如图3 所示的Eluer 区、RANS 区、LES 区。其中Eluer 区占大多数区域，包括远场与来流区域、图3 中的ER(Eluer Region) 区域，这些区域涡的影响较小，粘性力较小，因此被称为Eluer区；RANS 区域主要为近壁区，图3 中的RR(RANS region) 区域靠近壁面，粘性力占主要作用，因此被称为RANS 区；LES 区域主要为钝体后面的区域，图3中FR(Foucs Region) 与DR(Depature Region)，FR 为流体经过钝体后的尾涡区，这一区域由于剪切作用流场中存在很多细小的涡，DR 区为分离区，这一区域由于耗散作用涡比FR 区域要少。综上所述，在Eluer 区( 迎风与远场) 采用较为稀疏的网格，而在LES 区（背风）进行了网格加密。

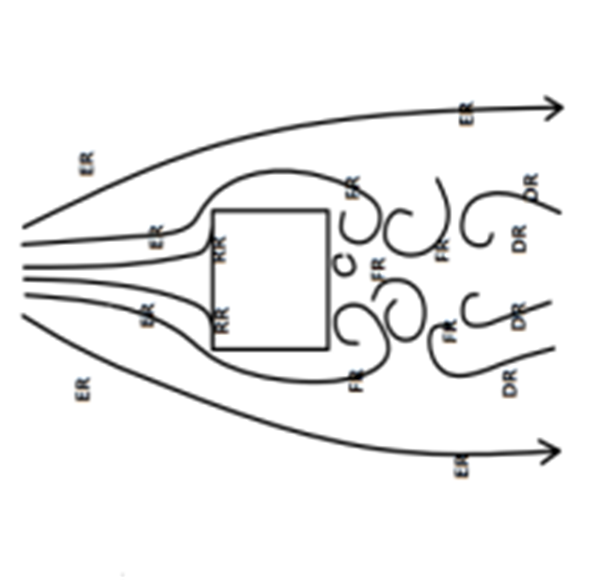
图3 钝体绕流的不同区域

本文根据这一分区对网格进行加密，其中迎风区的网格较为稀疏，并对尾涡区的网格进行加密。但是对于近壁处网格，当流体经过建筑物处受到逆压梯度的影响，产生较多的涡旋，RANS 和LES 需要采用不同的方法来解析这一区域的流场。

在RANS 模型中，当网格大小时, 公式(4)中的紊流应力，因此壁面处的网格将解析出有紊流的涡，为了避免这种现象解析中采用了壁面函数[13]方法，Δy+ 取值为：30<Δy+<200。其中Δy+ 可以通过Δy+=δyuτ/υ 得到，uτ 为壁面摩擦速度，可以通过uτ=Cμ0.25k0.5 估计。其网格如图4 所示。

另外在LES 模型中，当网格大小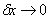时, 公式(4) 中的紊流应力，可以设置较小的网格来捕获所有的涡旋，采用Georgiadis[14] 给出的LES 的第一层网格的高度Δy+<1, 为了保证整体计算网格不能过大，采用网格加密技术，对近壁面网格加密如图5 所示。

图4  RANS 网格

图5  近壁面加密后的网格

2.5 紊流模型方程

2.5.1 RANS 模型

RANS 模型中: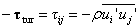，根据Boussinesq的假设：

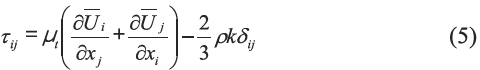
根据上述讨论，RNG k-ε 模型和SST k-ω 模型在建筑物绕流计算中具有优势，因此本次计算采用了这两种模型进行对比。

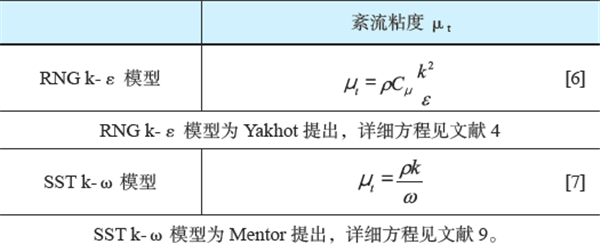
RNG k-ε模型计算中会过高地估计紊流剪切应力[12]，特别是存在逆压梯度会抑制壁面上流体的分离。而在绕流计算中通常会采用SST k-ω 模型进行计算，因此本文对比了这两种模型结果见表1。

表1 RANS模型

2.5.2  LES亚格子WALE模型

Smagorinsky[15] 提出，在小涡中紊流结构近似为各项同性的，因此可以利用Boussinesq 假设，同样有:

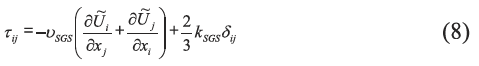
可以看到，接近壁面时如果存在速度梯度亚格子粘度并不为0，而实际中，壁面上并不存在紊流脉动，因此亚格子粘度应该为0。Von Direst[16] 采用壁面衰减函数来使得近壁处亚格子粘度为0，这一方法早期得到广泛应用，但是不适用于复杂的集合外形。Lilly[17] 提出了动态亚格子模型，这一模型式10 中的参数Ce 为通过求解输运方程得到，这样得到的近壁处的亚格子粘度为0，但是这一模型需要求解额外的方程，而且在某些情况下会变为负值[18]，因此本文没有采用上述两种方法，而是使用了WALE(Wall-Adapting Local Eddyviscosity)模型[19]。其亚格子粘度的定义和式9 一样，ksgs 的定义如下所示：

2.6 边界条件

RANS 的所有边界条件见表2。

Outlet： 在出口处采取下面边界条件: 即当速度大于零时，采用零梯度；当速度小于零时，采用固定值零。其他值见表1。

Front/Back： 采用了滑移边界，垂直于壁面的速度分量设置为固定值0，其速度分量设置为零梯度。在Up 面上:

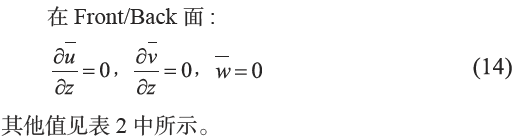
表2  RANS的边界条件

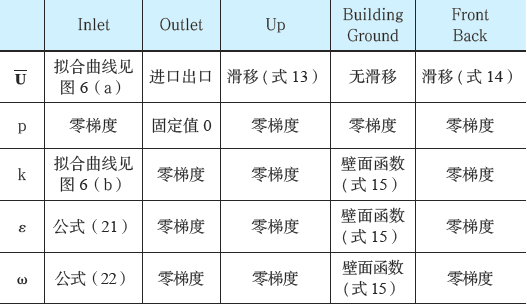
Building/Ground ：这两处边界为壁面，在RANS中，采用了壁面函数，根据Kim 和Moin[20] 的结论，当P 点满足30<yp+<300 时，壁面处无量纲速度u+ 满足log 率：

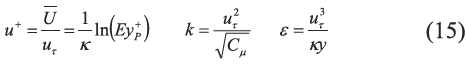
(15) 中Von Karman 常数为κ=0.41，对于光滑壁面其壁面粗糙系数E=9.8。

Inlet: 此边界为进口边界， 在RANS 中进口速度U、紊流能量k 可以直接拟合得到, 紊流耗散率则通过公式

如图6 所示。其中红点为文献10 中的实验值，蓝色实线为根据文献10 得到的拟合结果。(a) 为进口速度流向　的分量( 其他分量为0)，(b) 为紊流能量动能。压力在进口处则为零梯度。

LES 的所有边界条件见表3。

在LES 中Building/Ground 这两处边界为壁面[13]，第一层网格壁面高度Δy+<1，紊流可以得到完全解析，因此采用无滑移边界条件, 即速度为0。因为在壁面处的紊流脉动并不存在，因此这里的紊流粘度μt 为0。其他见表2。

图6 进口处拟合值与试验值

表3 LES的边界条件

而LES 的模拟自然进风紊流边界，由于计算的速度为滤波后的瞬时速度，对于其脉动速度的获得，目前主要有两类方法[21]：前驱方法和人造紊流进口。前驱方法是通过计算其他流场生成的紊流的某一截面，并以此截面数据来生成进口紊流，这种方法能生成的紊流包含了主要的紊流数据，例如具有相关关系和正确能谱的时间、空间脉动。这个单独的计算域通常是循环的槽道，但如前节所说，这种生成方法并不适合于本文。人造紊流进口目前主要有傅里叶方法[22]、主正交分解(Principal Orthogonal Decomposition/POD)方法[23]，本文采用了对高斯白噪声根据时间、空间相关关系进行滤波的方法。

Rij 为雷诺应力，可以根据试验值得到。

Xie 和Castro[26] 利用自相关系数得出了进口随时间变化的公式:

图7 左图为生成的高斯白噪声，右图为通过滤波放大后得到的初始进口速度，再利用所述的时间推进方法，就可以获得人造紊流了。

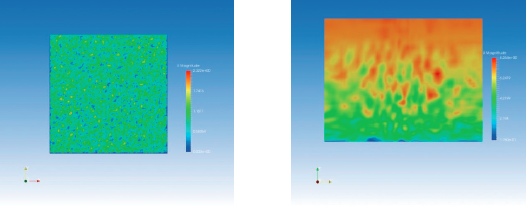
图7 　随机信号与进口边界

2.7 速度的平均值与方差

在CFD 计算中需要获得统计值，其中常用的有平均值和方差，其定义为：

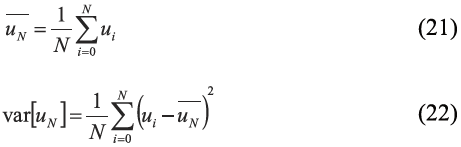
当u 为速度时: 　为N 步的平均速度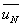，为N 步速度的方差，常用来表示速度脉动量的大小。CFD计算中一般仅使用当前时间步和上一时间步的值，因此会使用下面公式进行计算：

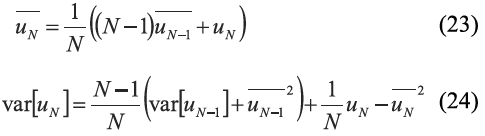
LES 计算中得到的是过滤后的瞬时速度，因此平均速度与速度脉动量可以直接利用式(23)、(24) 得到。对于非稳定RANS 模型（U-RANS 模型），由于只能得到时间步内的平均速度和平均紊流能量，总体平均速度和脉动速度需要通过下面方法得到：假设推进每个时间步内取N 个平均，总的时间步为M 步。假设　　为j个时间步内的平均速度，那么对总时间的平均速度根据式(21) 为:

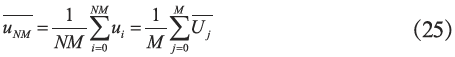
对总时间步的方差为：

2.8 差分格式与求解方法

所有计算格式见表4。

表4　 各项格式

LES 方法计算过程中，由于网格精度较高，保持库朗数小于1 需要浪费很多计算量，而如果时间步长较大并采用Euler 显式推进过程中，很容易发生发散，因此采用了隐式方法进行求解，其他部分均是采用了二阶或者三阶格式，来保证计算的精度。

压力速度的耦合方法采用了PISO 算法，迭代过程需要求解压力的泊松方程与速度修正方程，其中压力泊松方程采用GAMG 方法求解，速度修正方程采用PBICG( 预处理双共轭梯度) 方法，紊流能量与紊流粘度扩散率同样采用PBICG 方法求解。

3 计算结果与讨论

3.1 计算结果及其与实验值对比点的选取

本次计算结果如表5 所示，为了讨论LES 模拟时人造紊流边界对模拟结果的影响，也计算了没有加入人造紊流边界的LES 计算结果，WALE.1代表为加入人造紊流边界的WALE 模型LES 大涡计算结果, 用WALE.2代表为未加入人造紊流边界的LES计算结果。RNG k-ε模型与SST k-ω模型计算要比WALE大涡模型计算快很多，除了网格量小、时间步长更长外，还因为在LES 计算中在壁面附近采用了网格加密方法，导致产生了一定的四边形网格，因此每一步计算需要进行非正交修正，最后可以看到RANS 在计算资源上的优势明显。此外，在CPU 核数较少的情况下，加入并行计算也能非常快地提升计算效率。

表5 计算过程

实验记录[10] 了如图8 的坐标点数据，一共9 列，其都处于y/b=0 截面上，本次计算分别对比了这几条线上的平均值与脉动量值。

图8 实验选取的点

3.2 平均速度的对比

LES 的计算时间需要考虑计算结果的统计平均处理，针对这个建筑绕流的例子，考查了方柱绕流的斯特劳哈尔数Sr (f D/U) 为0.13 左右，以平均速度0.3m/s 来计算，计算平均时间需要大于其周期 (1/f≈0.2s)，因此所有的LES 计算选择的平均时间ΔT 为0.4s，包含了至少4 个周期以满足在做LES计算结果统计平均时的合理性要求。

图9 为不同模型y/b=0 截面上的平均速度与实验值的对比，其中红色方块为实验值，青色实线为RNG k-ε模型在ΔT 内的平均速度值, 黑色虚点为SST k-ω 模型在ΔT 内的平均速度值，灰色点线图为人造紊流进口的WALE.1 大涡模型结果，而绿色虚线为采用拟合实验值的进口速度、没有紊流脉动量的WALE.2 大涡模型结果。x 轴为平均速度，y 轴为高度z。实验值选取了图8中1-66 个点的数值，计算结果则选取了图8 中9 条线上模拟的结果。从图8 的9 条线上看，在迎风区以及建筑上部，如图9 (a)~(c) 所示，不同紊流模型的计算结果相差不大，同时由于这几条测量线靠近流入风的进口处，由实验值直接拟合得到的边界速度（不考虑紊流脉动）的WALE.2 大涡模型与RNG k-ε 模型、SST k-ω 模型都几乎与实验值重合，而加入了人造紊流的WALE.1 大涡模型会产生少量波动。但是在建筑物后方，当流体经过建筑物后由于逆压梯度的影响，产生了很多的涡旋。在这一区域，人造紊流进口的WALE.1 大涡模型与实验值非常接近。WALE.2 大涡模型的平均值结果与实验值也相差不大，但是由于进口处没有考虑紊流无法反应真实的流动情况，其结果在涡旋较多的区域结果出现了一定的误差。另外，时间平均紊流模型中的RNG k-ε 模型在建筑物后部(0.1m~0.2m) 处出现较大的误差，平均速度的结果小于实际值。这是由于RNG k-ε 模型过大地模拟了紊流剪切应力，当存在逆压梯度时会抑制建筑物表面流动的分离，在分离区的流体速度也会过小。而SST k-ω 模型在分离区的结果则与实验值吻合较好，但是在地面附近(0m~0.1m) 的结果与其他模型相比较差，速度平均值过大。从以上结果综合评价来看，在计算域的流入口处加入人造紊流的WALE.1 大涡模型的计算结果在建筑物后部与实验值结果吻合的最好。

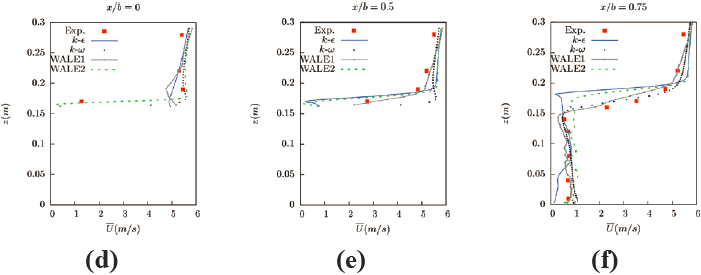
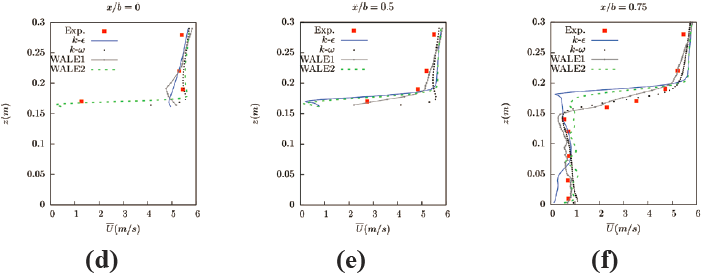
图9 y/b=0 界面平均速度与实验值的对比

如图10 所示(a)~(d) 依次为RNG k-ε 模型、SSTk-ω 模型、WALE.1 大涡模型加入人造紊流进口边界及WALE.2 大涡模型固定速度进口边界在z/b=0.125 截面上的ΔT 内平均速度分布。前两者的流线分布更加光滑，特别是RNG k-ε 模型和SST k-ω 模型的结果，在建筑物的后方形成了一对对称的涡结构，其中RNG k-ε模型如前文所述，由于其对流动分离的抑制作用，其结果在建筑物后部区域的涡覆盖的区域过大，平均速度因此也较小。SST k-ω 模型与RNG k-ε 模型相比于涡要小得多，结构的对称性也有一定的下降。另外，对于LES 的大涡模拟，具有加入人造紊流后的入口边界后的WALE.1 大涡模型和具有固定速度进口边界的WALE.2大涡模型的计算结果差异也比较大（图9 c/d），前者的计算结果形成的涡更加不对称，从和实验结果的比较来说后者更接近实际情况。

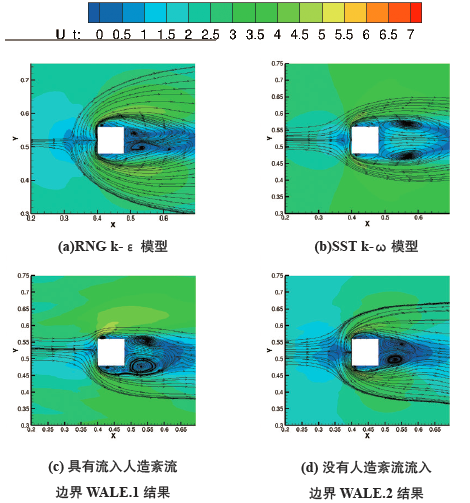
图10 z/b=0.125 界面上的平均速度

3.3 流场瞬时量的比较

图11 为RNG k-ε 模型在z/b=0.01 截面上的瞬时速度，建筑物后方随着时间的增加有交替的涡脱落现象。图12 为不同时刻SST k-ω 模型在z/b=0.01 界面上的瞬时速度，其后部同样也形成了交替的涡脱落。RNG k-ε模型相对于SST k-ω 模型其低速区的覆盖范围更大，涡结构也更明显，而后者涡结构不明显涡脱落的点也相对更早。

另外，因为大涡模拟是直接可以模拟瞬时速度，图13(a) 采用由试验值直接拟合得到速度作为流入进口边界速度（不考虑紊流脉动部分）的WALE.2 大涡模型在1.0s 的瞬时速度。 图13 (b) 为采用人造紊流脉动的流入进口边界速度的WALE.1 在1.0s 的瞬时速度。由两者对比可以看出，前者流体经过建筑物产生的涡比后者更小，而且并没有交替的涡脱落。后者由于在流入口加入了人工紊流，其模拟的涡不仅存在于建筑物后方，在进口也存在脉动，在全场也有不同速度的条带结构，这是因为在这一截面比较接近地面，流体在壁面处产生的紊流结构造成的。

图11 不同时刻RNG k-ε 模型在z/b=0.01 界面上的速度

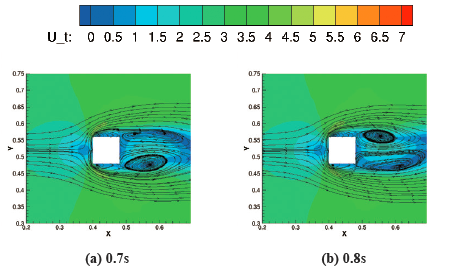
图12 不同时刻SST k-ω 模型在z/b=0.01 界面上的瞬时速度

图13 不同进口WALE 大涡模型在z/b=0.01 界面上的1.0s 时刻的瞬时速度

3.4 流场脉动量的比较

WALE 大涡模型计算可以直接采用公式(22)、(24)得到脉动量，而RANS 计算采用公式(24)、(26) 计算脉动量，对比了y/b=0 截面不同方向速度的脉动值与实验值对比如图11、图12、图13 所示，其中选取了y 轴同样为高度z，x 轴则为均方根速度　

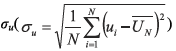
图14 为不同计算条件下流向脉动速度的对比，可以看到两种不同进口边界的LES 模拟中的WALE.1 和WALE.2 模型以及与RANS 模型中的RNG k-ε 模型与SST k-ω 模型差别较大。在图14(a) 中，RNG k-ε 模型与SST k-ω 模型由于根据进口的脉动速度直接拟合了一个紊流脉动量的流入口边界，而此处受进口边界的影响较大，因此其脉动速度与实验值最为接近。此外，在LES 模拟中，对于直接给定实验值拟合的固定进口速度( 没有紊流脉动量) 的WALE.2 模型，在流入进口区域其紊流脉动量几乎为零。而加入了人造紊流边界的WALE.1 的结果波动较大，但与实验值结果比较接近。图14(b)~(e) 为建筑上方的流向紊流脉动速度，这里RNG k-ε 模型与SST k-ω 模型的结果几乎都为相对稳定的值，这是由于这一区域仅存在各向同性的紊流能量k 产生的紊流脉动量；而在LES 中的对于没有紊流脉动量边界的WALE.2 的脉动量开始时几乎为零，随着紊流的往前发展，其紊流脉动量逐渐开始增加，特别是靠近建筑物壁面处的紊流脉动量，由于壁面处的紊流剪切应力流强度较大，产生了紊流的涡结构。另外，对于采用了人造紊流入口边界条件的WALE.1 的结果则与实验值几乎完全吻合，这一结果也说明了采用人造紊流入口边界是非常必要的也是非常适用于建筑绕流计算的。图14(f)~(i) 为建筑背风区的流向紊流脉动量的结果，RNGk-ε 模型与SST k-ω 模型的结果除了各向同性的紊流能量k 产生的脉动量外，其时间步内平均速度的脉动量不为零，因此其曲线也出现脉动的现象。而在LES 中，没有采用紊流脉动量边界的WALE.2 大涡模型结果，随着脱离进口边界的影响以及流体经过建筑时由于强剪切应力产生的涡脱落的影响，造成了较大的紊流脉动值，计算紊流脉动值也更加趋近于实验值，与之相对应的采用人造紊流边界的WALE.1 大涡模型结果也与实验值吻合较好，这是因为这两个部分图14(f)、图14(g) 靠近建筑物，网格密度较大计算结果也更精确。图14(h)、图14(i) 更加远离建筑物，对比图4 的网格密度，这一区域的计算结果也稍差。

图15、图16 为垂直流向与展向脉动速度的对比，这两个方向的脉动值趋势几乎是一致的，而这两个方向上计算结果都较为精确，特别是人造紊流边界的WALE.1 大涡模型结果，不仅仅在迎风区与实验值完全一致，在建筑物后方也几乎和实验值吻合较好。此外，RANS 的两种模型的结果在迎风区与背风区也与实验值更加一致，RANS 模型由于把流体看做各项同性在流向上有一定误差，但在其他方向上误差却并不大，因此可以把这两个方向看做各向同性，其结果甚至在一些截面要好于有人造紊流边界的WALE.1 大涡模型结果。但是如图所示，如果LES 模拟不采用人造紊流边界(WALE.2大涡模型)，其模拟结果也将不能得到一个稳定的光滑曲线，有些断面的结果可能甚至不如RANS 的模拟。

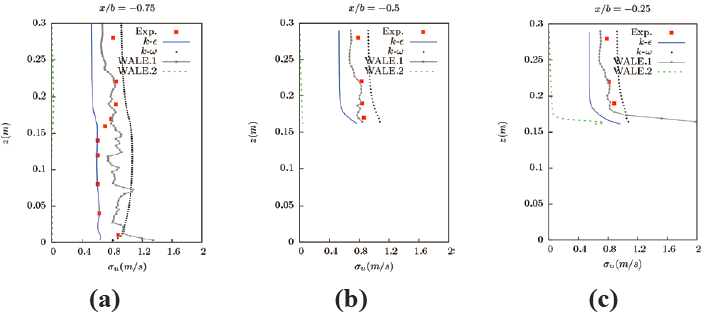
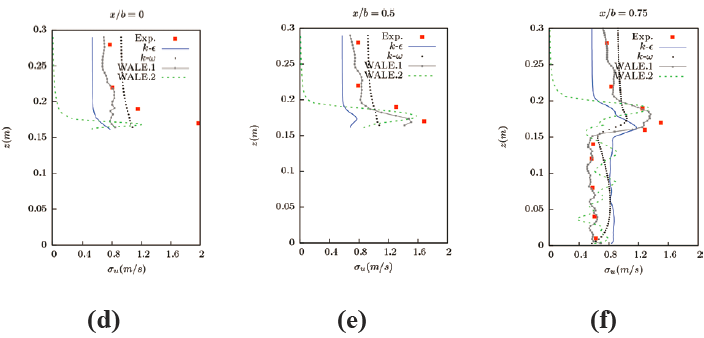
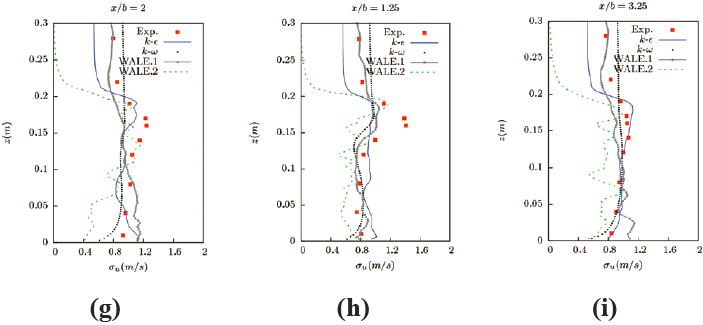
图14  y/b=0 界面流向脉动速度与实验值的对比

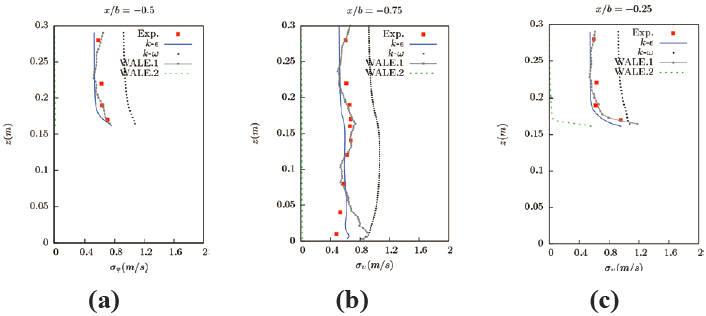
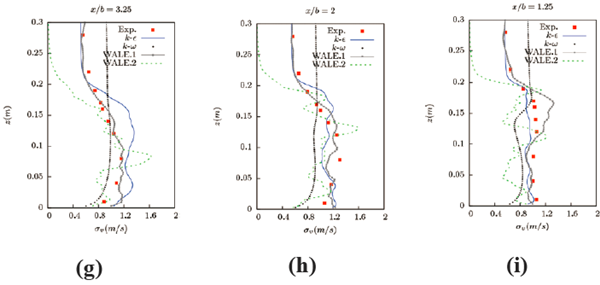
图15  y/b=0 界面垂直流向脉动速度与实验值的对比

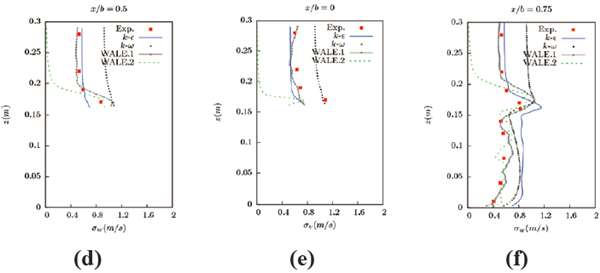
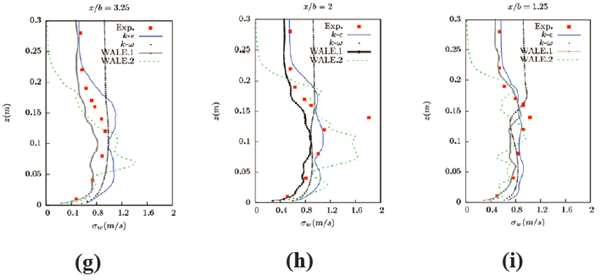
图16  y/b=0 界面展向脉动速度与实验值的对比

3.5 涡结构分析

为了对比不同计算结果的涡结构，采用Q 准则进行判定，其中Q 为速度梯度的二阶不变量:

图17 为Q=2000 的等值面，依次为RNG k-ε 模型、SST k-ω 模型的涡结构图，采用了公式(6)、(7) 中的紊流粘度μt 进行着色(0~1.5e-3)。以雷诺平均的定义，当时间步长很小时，有, 此时RANS 的雷诺平均方程趋向于N-S 方程，这样得到的涡结构为真实的涡结构。而在图17 中，RNG k-ε 模型的左右，因此能够得到较多的涡结构（图17（a）），而SST k-ω 模型的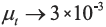左右，完全无法得到符合实际情况的涡结构，如图17(b) 所示。

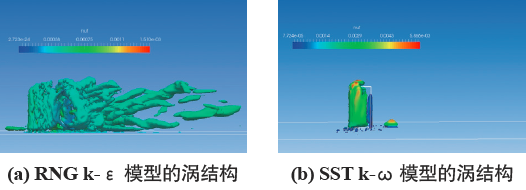
图17　RANS 下的涡结构

图18 为LES 模型得到的Q=2000 的等值面，依次为固定速度进口WALE.2 模型（图18 左图）与人造紊流进口的WALE.1 模型的涡结构图( 图18 右图），采用了公式(9) 的亚格子粘度进行着色μsgs(0~2e-5)，可以看到在壁面附近处的亚格子粘度非常小，这是因为LES 采用网格隐式滤波，当壁面处的网格尺度是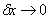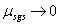，，此时空间滤波后的N-S 方程趋近于N-S 方程。这时得到的涡结构更符合实际情况。图18 中在壁面附近的涡也比较符合实际情况。而图18 的左图的WALE.2 在进口处没有加入脉动量，因此无法得到任何的涡结构，与实际结果相差较大。加入了人造紊流进口的WALE.1 的结果则更准确。如图4 中的网格所描述，建筑后方较远处对计算影响不大，因此网格更粗，此时的亚格子粘度μsgs 也较大，因此得到的涡结构相对较差，图9、图14~ 图16 中WALE.1 与WALE.2都存在较小的误差。

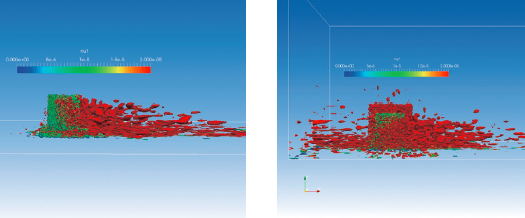
图18  LES下紊流粘度μt与涡结构

4 结论

本文研究了非稳态RANS 模型 (U-RANS) 与大涡模拟模型(LES/Large-Eddy Simulation) 计算2:1:1 建筑绕流问题，分析得到了非稳态RANS 模型 (U-RANS)中脉动速度的计算方法，对于大涡模拟模型(LES/Large-Eddy Simulation)，植入了新的计算域流入边界的紊流生成方法，并对比了不同流入紊流边界条件的LES模型。

各种紊流模型的计算平均量的总体结果都比较精确，特别是在迎风区与建筑物上方，与实验值都较为接近，但是在建筑物后方不同紊流模型的计算结果相差较大，RNG k-ε 模型在存在逆压梯度的区域会产生过高的紊流剪切应力，造成RNG k-ε 模型流动分离被抑制，其流动速度在建筑后方区域小于实际值。SST k-ω 模型的结果在漩涡区表现较好，但在壁面附近的结果则较差，同时会过高地计算紊流粘度，涡的结构表现的较差。WALE 大涡模型在不同流入边界条件处的结果都与实验值吻合得很好。

对于脉动量，RNG k-ε 模型在流向上与实验值有一定差距，其较小地估计了流向的脉动量，但在展向与垂直流向上的脉动值则比较精确；SST k-ω 模型的结果在流向的脉动速度与实验值相差不大，但在展向和垂直流向的脉动值的结果大于实验值，这两者在建筑物后方的模拟结果与实验值相差较大，并没有体现出脉动量的变化规律；LES 如果不加入人造紊流流入边界条件，由于完全没有给定流入脉动量，其模拟结果不如非稳态RANS 模型 （U-RANS）的计算，与实验值的差距较大；加入了人造紊流流入边界后的WALE 大涡模型（WALE.1）模拟结果比较精确，特别是在建筑物后方网格较为密集的区域，计算精度与变化趋势都与实验值吻合的很好。所有计算结果在展向和垂直流向方向的结果都相对较好，总体而言，加入了人造紊流流入边界条件的大涡模拟与实验值接近，其涡结构的表现也更符合实际情况。

参考文献

[1] 张维, 汤广发. 风对建筑绕流流动的数值方法[J].空气动力学学报, 1990(4):437-444.

[2] Y. Tominaga, A. Mochida, R. Yoshie, H. Kataoka,T. Nozu, M. Yoshikawa, et al., AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings, J. Wind Eng. Ind. Aerodynamics, 96(2008) 1749-1761.

[3] Tominaga Y, Stathopoulos T. Numerical simulation of dispersion around an isolated cubic building: Comparison of various types of k –ε, models[J]. Atmospheric Environment, 2009, 43(20):3200-3210.

[4] Yakhot V, Orszag S A, Thangam S, et al.Development of turbulence models for shear flows by a double expansion technique[J]. Physics of Fluids A, 1992,4(7):1510-1520.

[5] Tominaga Y. Flow around a high-rise building using steady and unsteady RANS CFD: Effect of large-scale fluctuations on the velocity statistics[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2015, 142:93-103.

[6] Werner H, Wengle H. Large-eddy simulation of turbulent flow over and around a cube in a plate channel[M].Springer Berlin Heidelberg, 1993.

[7] Tominaga Y, Mochida A, Murakami S, et al.Comparison of various revised k –ε, models and LES applied to flow around a high-rise building model with 1:1:2shape placed within the surface boundary layer[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2008,96(4):389-411.

[8] Eugene de Villiers. The potential of large eddy simulation for the modeling of wall bounded flows[D].London: Imperial College of Science, Technology and Medicine, 2006.

[9] Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. Aiaa Journal, 2012, 32(8):1598-1605.

[10] Meng Y, Hibi K. Turbulent measurements of the flow field around a high-rise building[J]. JWE, 2010,1998(76):55-64.

[11] Liu J, Niu J. CFD simulation of the wind environment around an isolated high-rise building: An evaluation of SRANS, LES and DES models[J]. Building & Environment, 2016, 96:91-106.

[12] Spalart P R, Streett C. Young-Person's Guide to Detached-Eddy Simulation Grids[J]. 2001.

[13] H K Versteeg, W Malalasekera. An introduction to computational fluid dynamics[D]. Pearson Education Limited, 2007.

[14] Georgiadis N J, Rizzetta D P, Fureby C. Largeeddy simulation: current capabilities, recommended practices, and future research[J]. Aiaa Journal, 2009, 48(8):1772-1784.

[15] Smagorinsky J S. Smagorinsky, J.: General circulation experiments with the primitive equations.monthly weather review 91, 99-165[J]. Monthly WeatherReview, 1963, 91(3):99-164.

[16] Van Direst, E.R. (1956). On turbulent flow near a wall, Aerosp. Sci. 23[J], 1007-1011.

[17] Lilly D.K. A proposed modification of the Germano subgrid‐scale closure method[J]. Physics of Fluids A: Fluid Dynamics (1989-1993), 1992, 4(3): 633-635.

[18] Fureby C., Tabor G., Weller H.G. A comparative study of subgrid scale models in homogeneous isotropic turbulence [J]. Physics of Fluids (1994-present), 1997, 9(5):1416-1429.

[19] Nicoud F, Ducros F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor[J]. Flow Turbulence & Combustion, 1999, 62(3):183-200.

[20] Moin P, Kim J. Numerical investigation of turbulent channel flow[J]. Journal of Fluid Mechanics, 2006,118(-1):1280-4.

[21] G.R. Tabor, M.H. Baba-Ahmadi. Inlet conditions for large eddy simulation: A review [J]. Computers & Fluids,39(2010) 553-567.

[22] Lee S, Lele S K, Moin P. Simulation of spatially evolving turbulence and the applicability of Taylorhypothesis in compressible flow[J]. Physics of Fluids A,1992, 4(7):1521-1530.

[23] Druault P, Lardeau S, Bonnet J P, et al. Generation of Three-Dimensional Turbulent Inlet Conditions for Large-Eddy Simulation[J]. Aiaa Journal, 2012, 42(3):447-456.

[24] Klein M, Sadiki A, Janicka J. A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulation [J]. Journal of Computational Physics, 2003, 186(2):652-665.

[25] Lund T S, Wu X, Squires K D. Generation of Turbulent Inflow Data for Spatially-Developing Boundary Layer Simulation [J]. Journal of Computational Physics,1998, 140(2):233-258.

[26] Xie Z T, Castro I P. Efficient Generation of Inflow Conditions for Large Eddy Simulation of Street-Scale Flows[J]. Flow Turbulence & Combustion, 2008, 81(3):449-470.

作者

杭州龙碧科技有限公司 王力 潘微 张维

欢迎订阅《建设科技》杂志（半月刊）

国内邮发代号：2-543

账   号：0200049309201072985

单位全称：北京康居认证中心

定   价：15元/本

开户银行：中国工商银行股份有限公司四道口支行

邮   箱：kcpc409@126.com

联系电话：010-88082199、010-88082202